How To Find Mode Of A Histogram
Primal Terms
o Measure out of fundamental tendency
o Average
o Mean (arithmetics mean)
o Way
o Median
Objectives
o Learn how to summate measures of central tendency--mean, median, and mode
o Know what each measure of central tendency says about a data prepare
Lesson
To narrate or draw a data prepare, we must learn the meaning and purpose of several dissimilar types of statistical values. Two important statistics are measures of central tendency and dispersion. Every bit the name indicates, a measure out of central tendency attempts to describe the "center" of a data set--this centre might be the most common value, the value that lies in the centre of the range of values in the data prepare, or some boilerplate of the values in the information set. (You've probably heard of and used averages earlier; nosotros will here delve into averages and similar measures in greater detail.) This lesson is devoted to measures of central tendency; later, we volition also consider dispersion, which is a measure out of the "spread" of data around some centre, and asymmetry (skewness), which measures how data is "skewed" to either side of the center.
A data prepare such as that shown in the following histogram displays a adequately obvious center: the centre bar. If you are familiar with averages (means), yous can probably already indicate to the average of the data, which is the fundamental (and tallest) bar in the graph (assuming that the data values to which the bars stand for are evenly distributed, as would be the case in a histogram)
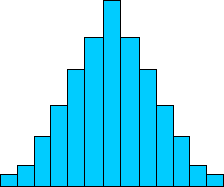
What if the data isn't symmetrically distributed, though? Consider the information set beneath.
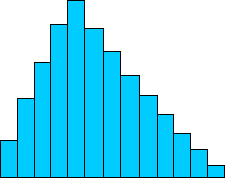
In this data gear up, the tallest elevation is not at the center. If you calculated the average of this data set, you'd also notice that the boilerplate doesn't correspond with the tallest peak. As a result, we must not but practise our math carefully, we must as well advisedly select what kind of math we exercise then that we accurately represent the data. Having shown why an average is non e'er the best statistic to use when characterizing a data ready, we tin can now turn to the definition and utilise of (this and) other measures of central tendency.
Mean (Average)
A mean (average) is perhaps the most well known measure of fundamental tendency. In baseball, fans might talk almost a bullpen'southward earned run average (ERA); students in a form might exist interested in their grade point average (GPA). The average (also called the arithmetic mean --this is the typical sense when simply the word hateful is used) of a data set is the sum of all the data values divided by the full number of values in the set up. Algebraically, a information set { 10 one, x ii, x iii,., xN } has a mean μ divers as follows:
![]()
(Notation that we use the Greek grapheme μ , indicating that this is a population hateful ; the same formula applies when computing the sample mean-- y'all might see the sample mean expressed using ![]() in this case, for instance. The bar annotation simply indicates a mean.) More more often than not, if we accept a prepare of values { x ane, 10 2, x iii,., 10N } with associated frequencies { f 1, f two, f 3,., fN } (think how nosotros divers a frequency in the previous lesson-here, we are simply proverb that the information value teni occurs fi times in the data fix), so we can ascertain the mean μ as follows:
in this case, for instance. The bar annotation simply indicates a mean.) More more often than not, if we accept a prepare of values { x ane, 10 2, x iii,., 10N } with associated frequencies { f 1, f two, f 3,., fN } (think how nosotros divers a frequency in the previous lesson-here, we are simply proverb that the information value teni occurs fi times in the data fix), so we can ascertain the mean μ as follows:
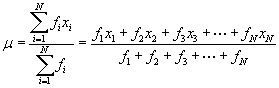
The numerator of this expression simply says that the sum consists of each value multiplied past the number of times it occurs in the data set up. The denominator is simply the total number of data values in the set (each value may occur more than once, so the denominator does not equal N ).
A mean is best suited to cases where the data are symmetrically distributed, as with the first bar graph shown above. If the data is skewed, as with the second bar graph above, the hateful is not as helpful. Consider the data tables below; the table on the left is a symmetrical distribution, like the outset bar graph, and the table on the right is a skewed distribution, like the second bar graph. (You may want to attempt graphing these distributions to get a sense of how the tables and graphs chronicle.)
| Information Value | Frequency |
| 1 | 1 |
| 2 | 2 |
| 3 | 4 |
| 4 | 8 |
| 5 | 16 |
| half dozen | 8 |
| 7 | iv |
| 8 | 2 |
| 9 | 1 |
Table 1
| Data Value | Frequency |
| i | 1 |
| 2 | vii |
| 3 | 20 |
| four | 15 |
| 5 | 12 |
| 6 | 9 |
| vii | 6 |
| 8 | 3 |
| 9 | one |
Tabular array 2
Using the mean formula for information with associated frequencies, we calculate the mean of the information in Tabular array 1 equally 5. The hateful for the information in Table ii is 4.38. Evidently, the hateful in the case of Table ane does a good chore of describing the information: the data value 5 is the most frequent value, and the other values show progressively lower frequencies. Thus, the mean shows the central tendency of the data set in this case. In the case of Tabular array 2, the mean doesn't do such a good chore: the most frequent value is 3, but the hateful is between two less frequent values (iv and five). As such, nosotros must consider other measures of central tendency for non-symmetric information sets.
Exercise Problem: Calculate the hateful of the following information set:
{1, 2, 3, 4, 5, vii, x, 15, 21, 22, 23, 24, 25, 26}
Solution : Just use the formula for the mean μ equally given above. The issue is the same regardless of whether the data corresponds to a population or a sample. Note that this data set contains xiv data values.
![]()
![]()
Thus, the mean of the information ready is most 13.4.
Way
The fashion is a measure of central tendency that corresponds to the about frequent data value. Referring again to the case information tables above, the fashion of the data in Table 1 is v, and the manner of the information in Table two is 3. The mode always selects the "summit" of the frequency graph. In some cases, withal, a data ready may have more than one value that is the fashion; this situation occurs when 2 or more values both have the same frequency and have the greatest frequency of whatsoever value in the ready.
Practice Problem: What is the way of the following data set?
{8, 1, 2, 0, three, 6, 2, 8, 4, 5, 6, 1, viii, half-dozen, 3, 9, 0, 9}
Solution : The way is the data value (or values) that occurs most frequently. One way to observe the mode is to draw a graph of the data (such every bit a histogram) and find the highest point on the graph. Alternatively, we tin lodge the data set and look to encounter which value is the mode.
{0, 0, ane, 1, 2, 2, 3, 3, 4, 5, 6, 6, 6, 8, 8, 8, 9, 9}
By inspection, we can see that both 6 and 8 represent to the style of the data set. Note that if each value in a information set occurs the aforementioned number of times, the style is not helpful.
Median
Another measure out of central tendency is the median. The median is the value that corresponds to the middle of an ordered prepare of data; that is to say, exactly one-half the data values in a prepare are beneath the median and exactly half are above the median. The easiest (conceptually, anyhow) method of calculating the median of a data set is to write the information in ascending order, then detect the eye value. If the data ready has an odd number of values, the median is a clear unmarried value; if the information fix has an fifty-fifty number of values, there is no single middle value. Instead, in this latter instance, the median tin can be defined every bit the hateful of the two middle values. Thus, given an ordered information set up { x 1, x 2, x 3,., 10Due north } with North members, we tin can write the median Grand algebraically as
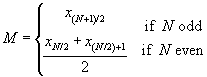
The median is a useful measure out of central tendency in cases where a few data values at one farthermost or some other accept a disproportionate event on the mean. Consider the information fix below, which might stand for to the incomes (in thousands of dollars) of a sure group of people.
{24; 42; 64; 38; 49; thirty; 34; 29; 2,350; one,932, 61, 52, 51, 19, 28}
This set has fifteen data values, so nosotros practise non need to summate a hateful of 2 middle values. To find the median, let'south first rewrite the data set in ascending lodge. Next, we'll place the middle value: this is the eighth data value, since there are seven values above information technology and seven values below it. The median is underlined in the ordered set below.
{nineteen; 24; 28; 29; xxx; 34; 38; 42; 49; 51; 52; 61; 64; 1,932; 2,350}
Allow'south now compare this result, 42, with the mean. Using the formula given above, we calculate the mean of this data set as approximately 320. Note advisedly that the mean in this example is well above the incomes of the majority of the people from whom these data were taken--simply ii people in the group brand at least the mean income, whereas 13 people (the vast majority) make far less than the mean income. The median income, however, does a much better job of expressing the central tendency of the information. If we were to ignore the two individuals with extremely high incomes, nosotros would find the hateful income of the remaining individuals to be about xl, which is shut to the median income.
A slightly more than difficult problem arises when the data values have associated frequencies; in such cases, writing a list of values may be quite hard, since the number of values can be large. However, the median can exist identified without also much difficulty if an ordered list of values and associated frequencies is either bachelor or is synthetic. We know that in an ordered list of N values, the median is the value that falls in the middle. If the ordered listing has associated frequencies, then the median is the value for which the cumulative frequency is N /2 (for even N ) or ( Due north + ane)/2 (for odd N ). Of course, the index ( N /2, for case) of the median may not be equal to the cumulative frequency of a particular value; the alphabetize of the median, nonetheless, must exist both less than the cumulative frequency of the median likewise as greater than the cumulative frequency of the immediately preceding value. This concept is best illustrated by example, so consider the following practice issues.
Practice Problem: Find the median of the information prepare below.
{102, 403, 729, 843, 920, 360, 842, 941, 357, 483, 207, 670, 471, 109}
Solution : Outset, order the information. Note that because the gear up has 14 members, the median is the mean of 2 fundamental values. These values are underlined in the ordered set beneath.
{102, 109, 207, 357, 360, 403, 471, 483, 670, 729, 842, 843, 920, 941}
At present, calculate the median Grand by finding the hateful of 471 and 483.
![]()
The median of this data set is thus 477.
Source: https://www.universalclass.com/articles/math/statistics/how-to-calculate-mean-median-mode.htm#:~:text=Solution%3A%20The%20mode%20is%20the,which%20value%20is%20the%20mode.
Posted by: alexanderabournat1975.blogspot.com


0 Response to "How To Find Mode Of A Histogram"
Post a Comment